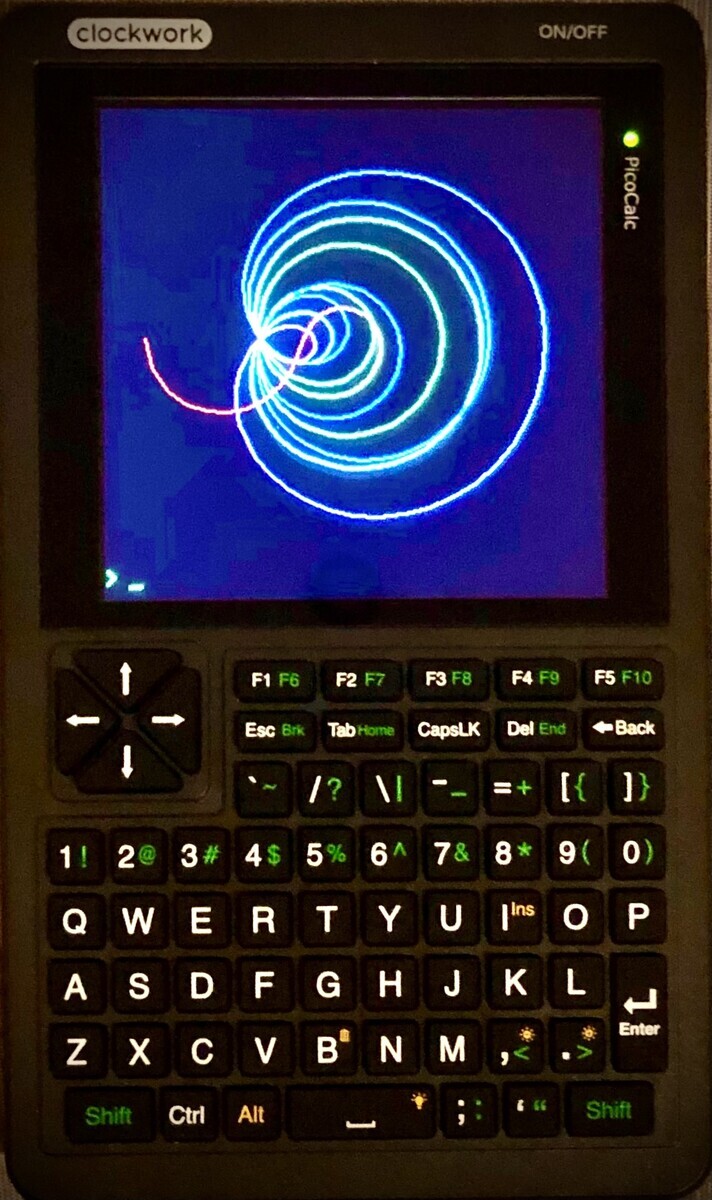
PicoCalc を購入しました。
PicoCalc

PicoCalc は Raspberry Pi Pico シリーズを搭載した 320x320 LCD とキーボードを備えたポケットサイズのコンピューターです。
非常にクールな見た目が良いですね。
Kit ($79) を注文して、2ヶ月ちょっとくらいで届きました。非常に良くできた作りで、各パーツをはめ込んでいけば10分くらいで完成できます。
Kit に付属している Pico 1 H には標準で MMBasic が動作する PicoMite という開発環境がファームウェアとして書き込まれており、付属のSDカードから Basic のサンプルコードを読み込んで試すことができます。
ボード上のPSRAMがAドライブ、SDカードはBドライブとなっているので、
B: files (ファイル一覧を表示) run "lorenz
と入力すれば実行されます。これはローレンツ方程式のカオス解を描画するプログラムで、最初の写真のような図形が描画されます。
F4 (EDITコマンド) を押すとプログラムコードを画面上でスクロールしてみたり編集も可能です。
MMBasicはインタプリタなので処理は遅いですが、それがまたノスタルジックでいい味を出しているように思います。
Basic はちょっと…ということなら MicroPython などのファームウェアもあるし、速度が欲しければ Arduino (C++) でもプログラミングは可能です。NES エミュレータなんかも付属していました。
リーマンゼータ関数のプロット
さて、最近『数学ガール/リーマン予想』を読みました。

その中で登場人物のリサが、リーマンゼータ関数 の
を動かした時の値を変化を複素平面上にプロットするということをやっていました。
これを自分でも見てみたいと思い、PicoCalcでも描画してみることにしました。
といっても、MMBasic は複素数計算にも対応していませんし、リーマンゼータ関数の値を級数計算で求めるのはかなりの計算量になるので、グラフが見たいだけなら決して向いている環境とは言えないのですが、果たしてどのくらいの速度で動くかにも興味があってのあえてのチャレンジです。
ζ関数の計算方法は以下の記事を参考にさせていただきました。
リーマンのゼータ関数で遊び倒そう (Ruby編) - tsujimotterのノートブック
比較的効率的に計算できるとされている下記の級数表示を使っています。
t = 0 〜 50 を 0.1刻みで描画した結果はこちら。単色だと動きが分かりにくいので t の変化をグラデーションカラーにしてみました。
いい感じです。
実行速度はマイコンを Pico 2 WH にアップグレードし、クロックスピードを OPTION CPUSPEED 250000000 で 250MHzにした状態でも8分もかかりました。めちゃくちゃ遅いけど複雑な動きをするので不思議と描画過程を見ていても飽きないです。
精度を犠牲にして LOWER_THRESHOLD を大きくすれば多少速くなりますが、複雑な収束の仕方をするのでやりすぎると局所的にひしゃげたりしてしまいます。
描画に使ったプログラムは末尾に置いておきますが、かなり生成AIで補完して楽をしています。
参考にした記事中のrubyコードでは nCm をキャッシュしたりして高速化していましたが、メモリが確保できなかったので普通に毎回計算しています。
描画結果は zeta.bmp というファイルに保存されるので、
load image "zeta
で再表示させることができます。